Hamming Weights of Integers
Easy
The Hamming weight of a number is the number of set bits (1-bits) in its binary representation. Given a positive integer n, return an array where the ith element is the Hamming weight of integer i for all integers from 0 to n.
Example:
Input: n = 7
Output: [0, 1, 1, 2, 1, 2, 2, 3]
Explanation:
| Number | Binary representation | Number of set bits |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 1 |
| 3 | 11 | 2 |
| 4 | 100 | 1 |
| 5 | 101 | 2 |
| 6 | 110 | 2 |
| 7 | 111 | 3 |
Lonely Integer
Easy
Given an integer array where each number occurs twice except for one of them, find the unique number.
Example:
Input: nums = [1, 3, 3, 2, 1]
Output: 2
Constraints:
numscontains at least one element.
Swap Odd and Even Bits
Medium
Given an unsigned 32-bit integer n, return an integer where all of n‘s even bits are swapped with their adjacent odd bits.
Example 1:
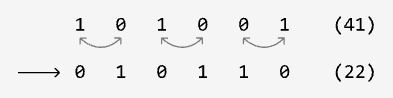
Input: n = 41
Output: 22
Example 2:
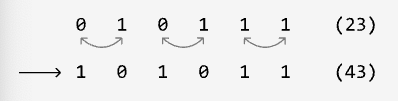
Input: n = 23
Output: 43